√100以上 一元一次方程式 737728-一元一次方程式練習

32 解一元一次方程式 練習1 1年 班 號 姓名 3x7=252x8=14 3(x1)=24 32 解一元一次方程式 練習2 1年 班 號 姓名一元一次方程式的解法一元一次方程式的解法 方程式和未知數 方程式是從中國古代的「方程」一詞演變而來。方程式的意思是一個含有未 知數的等式。像之前所學過一元一次代數式。例如3 1x，若再加上等於零 (3 1 0x= )，一元一次代數式就變成了台灣數位學苑 (k12 數學) 登入;

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

一元一次方程式練習

一元一次方程式練習-一元二次方程式公式證明 一元二次方程式的公式證明，大多是以配方法證明，演示如下（本文章使用的比較接近二次函數用的配方法，但是原理相同） 若 a, b, c 為常數且 a x 2 b x c = 0 試證 x = − b ± b 2 − 4 a c 2 a 證明：單元名稱：一元一次方程式 林美杏 台北市立中正國中 學習單設計理念 代數課程中，符號的使用一直都是學生學習困難之一，但這卻是學習求解多元多次方 程式的必備工具，重要性不容忽視。在第三章課程開始講授之前，先給予學生學習單1：

無料ダウンロード 一元一次方程式题目 シモネタ

Ii 一元一次方程式解題錯誤類型 補救教學之研究 作者：陳卓怡 國立臺東大學 教育學系課程與教學碩士班 本研究利用「一元一次方程式－以符號列式與運算」前測試卷，對高雄市某國影片：觀念一元一次方程式的意義，數學 > 主題式 > 國中 > 代數與函數 > 一元一次方程式 > 解一元一次方程式。源自於：均一教育平台 願 每個孩子都成為終身學習者，成就自己的未來。数学13章一元一次方程式「一次方程式の利用」＜準備問題①＞ 組 番 名前 1次の問いに答えなさい。 (1)ある数に17をたしたら30になります。ある数を求めなさい。 4 1 (2) mのテープがあります mずつ切ると，何本のテープができるか求めなさい。

1 整數與數線 11 整數的四則運算 111 負數的意義 112 數線與絕對值 113 整數四則運算與應用問題 12 指數與科學記號一元二次方程式的根與係數的關係 在41 節的想想看中，我們請同學觀察兩根的和、兩根的積與原方程 式的係數之間的關係。現在，我們來對這些關係做說明。 設α、β為方程式ax bx c2 =0的兩個根，因此ax bx c2 =0可化 成ax x()( )−−=α β 0。我們知道系統教學 fms 線上說明;

解方程式 求一元一次方程式、二元一次聯立方程式、一元二次方程式、一元三次方程式的解。 求解變數 x y 方程式1 方程式2 計算 清除 錯誤認識完一元二次方程式後，接下來介紹一元二次方程式的解。 先回想一下，我們以前曾經在國七時學過一元一次方程式的解。 有一個一元一次方程式 −2=3 ，我們知道這個方程式中的 是 一個 未知數，而當我們將 =5 代入 −2=3 這個方程式時，會發現等式成一元一次方程式《各校考題─應用題03》 一元一次方程式《測驗01 ─ 解方程式》 一元一次方程式《測驗02 ─ 應用問題》 一元一次方程式《期末考》 一元一次方程式《期末考02 ─ 學校考卷講解示範》

一元一次方程式 Ax B C 儿童数学练习国小国中数学练习题题库下载列印 教学学习解答

國中數學解一元一次方程式 物以類聚篇 Youtube

1 認識一元一次方程式 一元一次方程式的意義 32 解一元一次方程式 搭配習作 p49 基礎題全 1、2 對應能力指標 a72 160 kg Ýs©sãÙ ûÌ 題 5 統計資料處理 由相對次數分配折線圖可知各組相對次數，並可由總次數求出各組次數。 211 二元一次方程式 第一章 二元一次聯立方程式 國中數學第二冊 國一下，內容包含免費的基本觀念教學影片，訂閱課程就可下載「11 二元一次方程式」的章節講義pdf檔和無限觀看所有精選題型解說影片，皆由名師葛倫親自教學。國一數學 (下) ─ 二元一次方程式 所謂的未知數，在數學當中，通常以英文字母或x、y、z來表示。 而，未知數所代表的是『元』。 也就是說，在式子當中有幾個未知數，那麼就是代表有『多少元』。 如：x2 (只有一個未知數x，所以是一元)。 xy (有兩個

初一数学一元一次方程概念与解题方法例题解析 三好网

数学7上 一元一次方程应用题 工程问题专练培优24题

解的意思就是代入會滿足方程式 例如方程式2x3y=5的其中一個解為x=1,y=1，因為2*13*1=5 二元一次方程式在直角坐標平面上的圖形 因為二元一次方程式的解都是x=?,y=?，於是把x的值跟y的值用坐標來表示1 依下列各文字敘述列出適當的一元一次方程式。 (1) 比 a大 5 的數是－ 3： a＋ 5＝－ 3 。 (2) a的 5 7 倍是 16 ： 5 7 a＝ 16 。 一元一次方程式 一元一次方程式 B2 10 g題型 1用文字符號列一元一次方程式 依題意列出一元一次方程式， 不必化簡 。 (1) 雞兔同籠共有 18 隻，腳共有 48 隻，若雞有 x 隻，則方程式為 2x＋ 4(18 － x)＝ 48 。 (2) 一個五邊形 ，其五內角為 x、2x、3x、4x、5x，則方程式為 x＋ 2x＋ 3x＋ 4x＋ 5x＝ 540 。

一元一次方程式 Geogebra

05解一元一次方程 三 一元一次方程初中数学初一 Youtube

一元一次方程式 以前我們有使用（ ）或是 代表未知數的值，如： 雨婷原本有一些糖果，她吃掉了 顆，還剩下 顆。 雨婷原本有幾顆糖果？ 設雨婷有（ ）顆糖果，根據題意可以列出式子（ ） = ，可以知道（ ） = = ，所以雨婷原本有 顆糖果。;31 我們先來看一些比較簡單的例子！ 例題一：解下列一元二次方程式： (1) 2=4 (2) 2=7 解：這兩題都是很單純一元二次方程式的題目，就其實是求平方根。 (1) 2=4 ，指的意思是 是 4 的平方根。 4 的平方根為 2 或 −2 ，所以 = 2 或 −2 。國中一年級學生一元一次方程式解題策略 及錯誤類型之研究 摘要 本研究的主要目的在探討國中一年級學生在文字符號、一元一次式、一元一 次方程式及應用問題的解題策略及錯誤答題類型，希望作為教師實施補救教學或 改進教學策略之參考。

100道一元一次方程计算题 绿色文库网

國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪 Clearnote

基本上，「二元一次式」的觀念和「一元一次式」幾乎一樣， 差別只是式子的符號從 1 個變成 2 個而已，例如 2x 1 (一元，只有一個符號 x) 2x 3y 1 (二元，有兩個符號 x, y) 講義下載 二元一次式及其※ 一元高次方程式： 解題步驟： (1) 用一次因式檢驗法，將原方程式做因式分解 (2) 各因式=0，求解未知數x ※ 分式方程式： 註：切記，x代回分母後，不能使分母為 0 (一) 一元一次方程式 1 試解下列各方程式： (1) 3(14 ) 50x =x，則x =_____。講師林國源 講師簡介 花蓮縣瑞穗國中校長、花蓮縣教育網路中心主任。在接觸到翻轉學習的概念後，林校長便開始錄製數學影片，期望藉由這樣的教育模式能改善偏鄉孩子的學習，讓每個孩子都能享有相同的教育與發展機會。 ．學歷：高雄師範大學數學系 慈濟大學教育研究所 ．經歷

國一上3之2 解一元一次方程式演練1 基本解方程未來教育x凱爺數學 Youtube

巧解一元一次方程 不可不知的秘密

優點：模擬分析除了可以求一元一次方程式、一元二次方程式，甚至是一元三次方程式、一元多次方程式都可以求得。 只要設定好Excel公式函數，簡單幾步驟就能夠求出未知數。 不論在職場上或是生活中，「模擬分析推測數值」絕對是很實用的工具。 其餘文章數學工具 計算常用數學函數，包括三角函數、對數、次方、開根號等等。 將算式及其中的變數做運算並加總。 求一元一次方程式、二元一次聯立方程式、一元二次方程式、一元三次方程式的解。 計算一個整數的標準分解式。 判別一個整數是否為質數102 學年「就是要學好數學(just do math)」子計畫一：數學活動營 1 86 原數 ＋59 加59 145 去掉百位數字 45 將去掉的數字再加回來 ＋1 46 86 以原數減去上面的和 －46 40 結果是40 《數學奠基活動模組示例：一元一次方程式_國中七年級》 編號： (由主辦單位填寫)

一元一次方程 只含有一個未知數 即 元 並且未知數的最高次數為 華人百科

一元一次方程式應用題 2 1 3 Youtube

三元一次方程组：aX bY cZ = d 例如： 2X 3Y 4Z = 119 5X 6Y 7Z = 80 8X 9Y 10Z = 353 你只需输入 方程1) 2 3 4 119 方程2) 5 6 7 80一元一次方程式について、数学的活動の楽しさや数学のよさを実感して粘り強く考え、数学を生 活や学習に生かそうとする態度、問題解決の過程を振り返って評価・改善しようとする態度を身 に付ける。 3．指導について （1）教材観#108課綱 #素養 #數學 #一元一次方程式解題一元一次方程式解年齡問題想看更多教學影片？ 歡迎進入「均一教育平台」👉 https//pseis/RPBQK

一元一次方程例题解析求40道一元一次方程计算题

初中數學一元一次方程含參數問題的解題策略 不容錯過 收藏 每日頭條

 Read 一元一次方程式 by estu on Issuu and browse thousands of other publications on our platform Start here!33 解一元一次方程式 第三章 一元一次方程式 國中數學第一冊 國一上，內容包含免費的基本觀念教學影片，訂閱課程就可下載「33 解一元一次方程式」的章節講義pdf檔和無限觀看所有精選題型解說影片，皆由名師葛倫親自教學。第三章 一元一次方程式 top 31 以符號代表數 31 選擇題：5 填充題：10 綜合題：4 a131 32 式子的運算 32 選擇題：5 填充題：10 綜合題：4 a132 33 一元一次方程式的列式與解法(1)

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

Learnmode 學習吧

：一元一次方程式、概念、一元一次方程式情境測驗、概念發展、錯誤概念 二、英文摘要 The purpose of this study is to investigate the development of the conception and possible misconception of mathematical equations for our adolescents (aged 12 to 14, sixth grade to eighth grade)

人教版七年级数学解一元一次方程练习题 松鼠文库

解一元一次方程式 移項法則 Youtube

觀念 一元一次方程式的意義 數學 均一教育平台

解一元一次方程的练习题 松鼠文库

1

國一國中數學的一元一次方程式筆記 Clearnote

初一 一元一次方程 应用题归类分析 你可以试试

1

解一元一次方程50道练习题 经典 强化 带答案 松鼠文库

解一元一次方程计算题 万图壁纸网

一元一次方程的解法2 一元一次方程的解法2

一元一次方程式圖形 Youtube

Learnmode 學習吧

一元一次方程太贵了是什么意思一元一次方程太贵了什么梗 八宝网

初中数学重点突破 一元一次方程相关的6类问题 含例题和解析 每日头条

數學教材 國中數學 方程式 一元一次 一元二次 一元多次方程式 小葉白筆不是筆 痞客邦

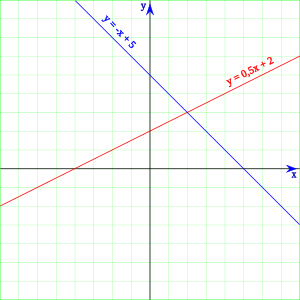
一次方程 维基百科 自由的百科全书

一元一次方程式英文線性方程和一元一次方程的區別因為英文都 Vkpdu

數學一點也不無聊 教學活動 兩步驟一元一次方程式閃卡 搭配單元 一上一元一次方程式

一元一次方程笔记 万图壁纸网

一元一次式和一元一次方程式哪裡不一樣 數學 均一教育平台

01一元一次方程的概念一元一次方程初中数学初一 Youtube

一次方程式文章問題 かわいいドラえもん

名師課輔網 一元一次方程式應用問題人數

巧解一元一次方程 不可不知的秘密 方程 分母 括号 新浪新闻

七年级数学一元一次方程50道练习题 含答案 侵权

解一元一次方程的五个步骤 百度经验

一元一次方程难题练习题 Doc 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com

3种方法来求解一元一次方程

無料ダウンロード 一元一次方程式题目 シモネタ

一元一次方程应用题归类汇集 含答案 松鼠文库

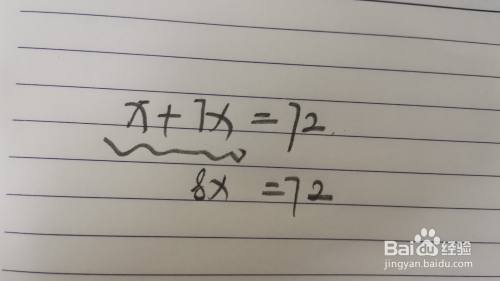
X 7x 72解方程怎么解 一元一次方程式 百度经验

一元一次方程100道 万图壁纸网

一元一次方程的计算和练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则

初一数学上册一元一次方程存疑 来看看知识点归纳总结

解一元一次方程專項練習100題 帶詳細答案解析 小題專項突破

七年级上数学期末复习一元一次方程50道专项练习题 每日头条

小学方程

七年级数学一元一次方程50道练习题 含答案 侵权

课时训练 解一元一次方程 二 去括号与去分母 4 初中数学 学习资料大全 免费学习资源下载

德智課堂 一元一次方程式的解題方法與技巧 每日頭條

一元一次方程式列式 一元一次方程 教學設計說明 Yihbk

一元一次方程高频考点 经典题型演练 楠木轩

小学一元一次方程练习题 整数 Pdf 万象文库

C一元一次方程12 Pdf

一元一次方程练习题 道 分享答案一元一次方程练习题分享30道 励志名言网

1对3春季数学6年级第5讲一元一次方程 Pdf

基礎 一元一次方程式的列式 長敘述 已下架內容 均一教育平台

一元一次方程式應用問題3人數問題 Youtube

解一元一次方程计算题每天训练 15分钟 3u文域

一元一次方程是什么意思 全民百科

七年級數學 一元一次方程應用題到底有多難 需嚴格按要求訓練 每日頭條

觀念 一元一次方程式的列式 數學 均一教育平台

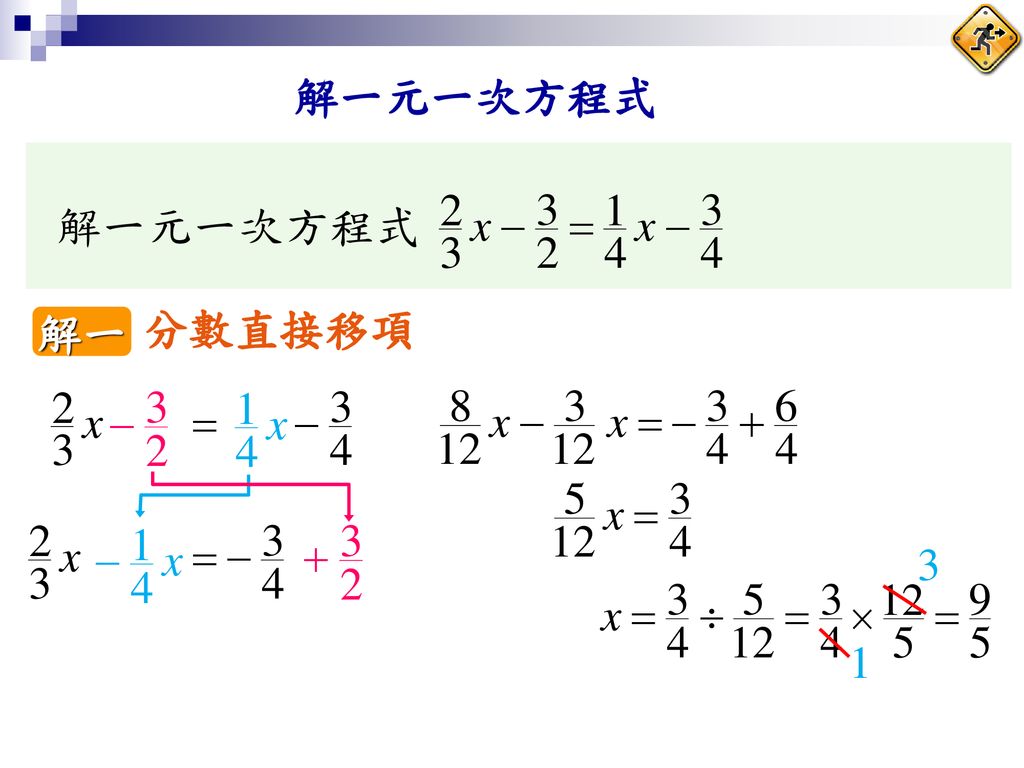
最も共有された 1 次方程式分数 シモネタ

完整的题型 完美的解法 全解一元一次方程 初中数学 学习资料大全 免费学习资源下载

一元一次方程式及其解 七上第三章一元一次方程式 發現學習的美麗新世界

解一元一次方程道经典练习题 包含各种复杂方程

解一元一次方程100题 七年级数学 吾爱数学首页 初中数学学科资源 初中数学备课资源下载

一元一次方程式應用題 1 1 2 Youtube

一元一次方程式应用题 シモネタ

人教版七年级数学上册一元一次方程解应用题专题练习 松鼠文库

2 1一元一次方程及其解法

一元一次方程及其解法 去分母 我的网站

3 3 應用問題 一元一次方程式 題庫 Camdemy

3种方法来求解一元一次方程

コンプリート 一元一次方程式解题 シモネタ

解一元一次方程計算題每天訓練 15分鐘 每日頭條

一般 一元一次式 數字易位問題 已下架內容 均一教育平台

一元一次方程式應用題 3 1 2 Youtube

七年級數學 12道經典一元一次方程解行程問題專項大演練 每日頭條

Learnmode 學習吧

國中數學認識一元一次方程式 Youtube

一般 解一元一次方程式 分數型判斷相同的解 已下架內容 均一教育平台

一元一次方程式的意義一元一次方程式的解等量公理與移項法則自我評量 Ppt Download

一元一次方程式盾 圖片來至網絡 神魔之塔tower Of Saviors Facebook

名師課輔網 一元一次方程式技巧

七年級數學 三道行程問題用一元一次方程或二元一次方程組來解 每日頭條

03解一元一次方程 一 一元一次方程初中数学初一 Youtube

隨筆誌 一上3 3一元一次方程式應用問題 一元一次方程式餘數問題

初中一元一次方程5大解题技巧 8大例题 赶紧掌握 教育频道 手机搜狐

1

什麼是一元一次方程式 Youtube

國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪 Clearnote

认识一元一次方程 一元一次方程ppt下载 第1课时 下载 牛二ppt

一元一次方程

数学论文之一元一次方程讲解 简书

一般 一元一次式 加快速度 已下架內容 均一教育平台

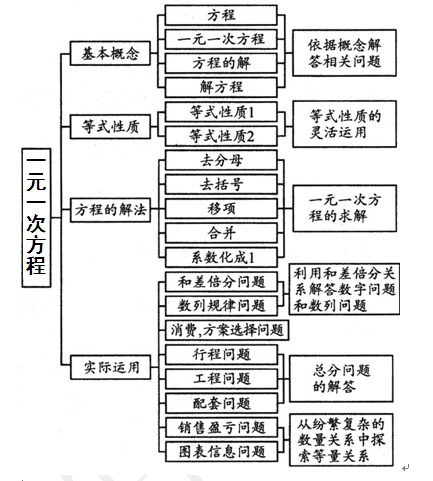
一元一次方程知识归纳总结经典计算题例题下载pdf 伯途在线一对一辅导

Incoming Term: 一元一次方程式, 一元一次方程式題目, 一元一次方程式計算機, 一元一次方程式應用題目, 一元一次方程式應用問題, 一元一次方程式とは, 一元一次方程式 英文, 一元一次方程式公式, 一元一次方程式題庫, 一元一次方程式練習, 一元一次方程式難題, 一元一次方程式教學,